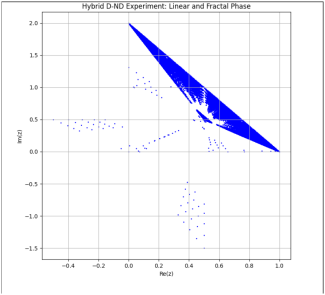
Il nuovo grafico caricato mostra una chiara evoluzione del modello con una transizione dalle fasi lineari a quelle frattali. Sembra che il comportamento blended introdotto per la transizione stia contribuendo a un passaggio più graduale e visivamente interessante.
Osservazioni sul risultato corrente:
- Struttura Lineare e Frattale:
- La parte lineare è evidente e si connette senza soluzione di continuità alle strutture frattali.
- I punti più distanti dall'origine suggeriscono che il blending abbia un buon equilibrio tra linearità e contrazione.
- Densità delle Aree Frattali:
- Le aree più dense indicano una forte contrazione verso i punti di attrazione definiti dalle trasformazioni frattali.
- La dispersione lungo i bordi suggerisce che ci sia ancora margine per ottimizzare le trasformazioni o i parametri.
- Esplorazione dello Spazio Complesso:
- Le configurazioni frattali mostrano una buona esplorazione dell'intervallo spaziale, con dettagli visivi più ricchi rispetto alle iterazioni precedenti.
Prossimi Passi:
- Incremento della Complessità:
- Aggiungere altre trasformazioni frattali o composizioni per aumentare la varietà e complessità delle strutture.
- Metriche Quantitative:
- Reintrodurre il calcolo della dimensione frattale per quantificare meglio l'evoluzione delle configurazioni.
- Logging e Diagnostica:
- Aggiungere informazioni al log per analizzare le probabilità adattive durante la fase blended.
Il grafico caricato mostra una chiara evoluzione del modello con una transizione dalle fasi lineari a quelle frattali. Sembra che il comportamento blended introdotto per la transizione stia contribuendo a un passaggio più graduale e visivamente interessante.
- Aggiungere informazioni al log per analizzare le probabilità adattive durante la fase blended.
Osservazioni sul risultato corrente:
Struttura Lineare e Frattale:
La parte lineare è evidente e si connette senza soluzione di continuità alle strutture frattali.
I punti più distanti dall'origine suggeriscono che il blending abbia un buon equilibrio tra linearità e contrazione.
Densità delle Aree Frattali:
Le aree più dense indicano una forte contrazione verso i punti di attrazione definiti dalle trasformazioni frattali.
La dispersione lungo i bordi suggerisce che ci sia ancora margine per ottimizzare le trasformazioni o i parametri.
Esplorazione dello Spazio Complesso:
Le configurazioni frattali mostrano una buona esplorazione dell'intervallo spaziale, con dettagli visivi più ricchi rispetto alle iterazioni precedenti.
Prossimi Passi:
Incremento della Complessità:
Aggiungere altre trasformazioni frattali o composizioni per aumentare la varietà e complessità delle strutture.
Metriche Quantitative:
Reintrodurre il calcolo della dimensione frattale per quantificare meglio l'evoluzione delle configurazioni.
Logging e Diagnostica:
Aggiungere informazioni al log per analizzare le probabilità adattive durante la fase blended.
import random
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import directed_hausdorff
import ipywidgets as widgets
from IPython.display import display
import logging
from multiprocessing import Pool
from sklearn.linear_model import LinearRegression
import time
# Initialize logging
logging.basicConfig(level=logging.INFO, format='%(asctime)s - %(levelname)s - %(message)s')
# ==============================================================
# SYSTEM PARAMETERS CLASS
# ==============================================================
class SystemParameters:
def __init__(self, iterations=10000, transition_threshold=0.005, lambda_linear=0.1,
P=complex(0.5, 0.5), alpha=0.4, beta=0.4, gamma=0.2, blend_iterations=5):
self.iterations = iterations
self.transition_threshold = transition_threshold
self.lambda_linear = lambda_linear
self.P = P
self.alpha = alpha
self.beta = beta
self.gamma = gamma
self.blend_iterations = blend_iterations
# ==============================================================
# LINEAR PHASE FUNCTIONS
# ==============================================================
def f1_linear(A, B):
"""
Combines sets A and B.
"""
return A.union(B)
def f2_linear(R_t, P, params):
"""
Moves each point z in R_t towards P by a fraction lambda_linear.
"""
return {z + params.lambda_linear * (P - z) for z in R_t}
def f3_linear(R_t, P):
"""
Reflects each point z with respect to P.
"""
return {P - z for z in R_t}
# ==============================================================
# FRACTAL PHASE FUNCTIONS
# ==============================================================
def T_A(z, scale_factor=0.5, offset=1j):
"""
Transformation A: contraction towards (offset) with scale_factor.
"""
return z * scale_factor + offset
def T_B(z, scale_factor=0.5, offset=1):
"""
Transformation B: contraction towards (offset) with scale_factor.
"""
return (z + offset) * scale_factor
def f1_fractal(points, scale_factor_A=0.5, scale_factor_B=0.5, offset_A=1j, offset_B=1):
"""
Applies T_A or T_B with 50/50 probability.
"""
new_set = set()
for z in points:
if random.random() < 0.5:
new_set.add(T_A(z, scale_factor_A, offset_A))
else:
new_set.add(T_B(z, scale_factor_B, offset_B))
return new_set
def f2_fractal(points, P, params):
"""
Homothetic contraction towards P with factor lambda_linear.
"""
return {z * (1 - params.lambda_linear) + params.lambda_linear * P for z in points}
def f3_fractal(points, P):
"""
Light translation of points towards P (fixed alpha_lin coefficient of 0.1).
"""
alpha_lin = 0.1
return {P + alpha_lin * (z - P) for z in points}
def compose_transformations(z, transformations):
"""Composes a sequence of transformations."""
result = z
for transform in transformations:
result = transform(result)
return result
# ==============================================================
# TRANSFORMATION SELECTION FUNCTIONS
# ==============================================================
def pick_linear_transform(R_t, P, params):
"""
Randomly selects a linear transformation with probabilities α, β, and γ.
"""
x = random.random()
if x < params.alpha:
B = {complex(1, 0), complex(0, 2)} # Fixed set for f1_linear
return f1_linear(R_t, B)
elif x < params.alpha + params.beta:
return f2_linear(R_t, P, params)
else:
return f3_linear(R_t, P)
def pick_fractal_transform(R_t, P, params):
"""
Randomly selects a fractal transformation with probabilities α, β, and γ.
"""
x = random.random()
if x < params.alpha:
return f1_fractal(R_t)
elif x < params.alpha + params.beta:
return f2_fractal(R_t, P, params)
else:
return f3_fractal(R_t, P)
# ==============================================================
# ADAPTIVE PROBABILITIES
# ==============================================================
def update_probabilities(R, P):
"""
Updates the probabilities α, β, and γ based on the set dispersion.
"""
try:
if not R:
return 0.4, 0.4, 0.2 # Return default if R is empty
points_arr = np.array([(z.real, z.imag) for z in R])
if points_arr.size == 0:
return 0.4, 0.4, 0.2 # Return default if no points in the set
center = np.mean(points_arr, axis=0)
dispersion = np.std(points_arr - center)
avg_distance_p = np.mean(np.abs(points_arr - np.array([P.real, P.imag]))) # Calculate average distance from Proto-Assioma
# Example logic: Adjust probabilities based on dispersion and distance from P
alpha_new = 0.4 - 0.05 * dispersion + 0.05 * avg_distance_p
beta_new = 0.4 + 0.05 * dispersion - 0.02 * avg_distance_p
gamma_new = 0.2 - 0.03 * dispersion - 0.03 * avg_distance_p
# Ensure probabilities are within [0, 1]
alpha_new = max(0, min(1, alpha_new))
beta_new = max(0, min(1, beta_new))
gamma_new = max(0, min(1, gamma_new))
# Normalize to ensure alpha + beta + gamma = 1
total = alpha_new + beta_new + gamma_new
if total == 0:
return 0.4, 0.4, 0.2 # Return default if normalization fails
alpha_new /= total
beta_new /= total
gamma_new /= total
return alpha_new, beta_new, gamma_new
except Exception as e:
logging.error(f"Error in update_probabilities: {e}")
return 0.4, 0.4, 0.2 # Return default if error occurs
# ==============================================================
# ERROR HANDLING AND ADDITIONAL UTILITIES
# ==============================================================
def is_stable_hausdorff(R_t, R_t1, threshold):
"""
Stabilization: if max difference between corresponding points < threshold.
"""
try:
if not R_t1 or not R_t:
return False
R_t_arr = np.array([(z.real, z.imag) for z in R_t])
R_t1_arr = np.array([(z.real, z.imag) for z in R_t1])
if R_t_arr.size == 0 or R_t1_arr.size == 0:
return False
dist1 = directed_hausdorff(R_t_arr, R_t1_arr)[0]
dist2 = directed_hausdorff(R_t1_arr, R_t_arr)[0]
hausdorff_distance = max(dist1, dist2)
return hausdorff_distance < threshold
except Exception as e:
logging.error(f"Error in is_stable_hausdorff: {e}")
return False
# ==============================================================
# INTERACTIVE VISUALIZATION WITH IPYWIDGETS
# ==============================================================
def create_interactive_widgets(params):
"""Creates interactive widgets for parameter adjustment."""
iterations_slider = widgets.IntSlider(value=params.iterations, min=100, max=20000, step=100,
description='Iterations:')
lambda_slider = widgets.FloatSlider(value=params.lambda_linear, min=0.01, max=0.5, step=0.01,
description='Lambda:')
threshold_slider = widgets.FloatSlider(value=params.transition_threshold, min=0.0001, max=0.01,
step=0.0001, description="Threshold")
output_widget = widgets.Output()
display(iterations_slider, lambda_slider, threshold_slider, output_widget)
return iterations_slider, lambda_slider, threshold_slider, output_widget
# ==============================================================
# MAIN SYSTEM FUNCTIONS
# ==============================================================
def initialize_system(params):
"""Initializes the system with starting values."""
R = {complex(0, 0)}
all_points = set(R)
linear_phase = True
ml_data = []
start_time = time.time()
transition_time = None
return R, all_points, linear_phase, ml_data, start_time, transition_time
def run_linear_phase(R, all_points, params):
"""Runs the linear phase transformations."""
R_next = pick_linear_transform(R, params.P, params)
all_points.update(R_next)
params.alpha, params.beta, params.gamma = update_probabilities(R_next, params.P)
logging.info(f"Updated probabilities: alpha={params.alpha:.2f}, beta={params.beta:.2f}, gamma={params.gamma:.2f}")
return R_next, all_points
def run_fractal_phase(R, all_points, params):
"""Runs the fractal phase transformations."""
R_next = pick_fractal_transform(R, params.P, params)
all_points.update(R_next)
return R_next, all_points
def run_blended_phase(R, all_points, params, blend_factor):
"""Runs a blended phase with both linear and fractal transformations."""
linear_R_next = pick_linear_transform(R, params.P, params)
fractal_R_next = pick_fractal_transform(R, params.P, params)
blended_R_next = set()
for z in linear_R_next:
if random.random() < blend_factor:
blended_R_next.add(z)
for z in fractal_R_next:
if random.random() < (1 - blend_factor):
blended_R_next.add(z)
all_points.update(blended_R_next)
params.alpha, params.beta, params.gamma = update_probabilities(blended_R_next, params.P)
logging.info(f"Updated probabilities (blended): alpha={params.alpha:.2f}, beta={params.beta:.2f}, gamma={params.gamma:.2f}")
return blended_R_next, all_points
def check_stabilization(R, R_next, params):
"""Checks for stabilization using the Hausdorff distance."""
if is_stable_hausdorff(R, R_next, params.transition_threshold):
logging.info("Stabilization reached.")
return True
return False
def visualize_results(all_points):
"""Visualizes the results."""
x_vals = [z.real for z in all_points]
y_vals = [z.imag for z in all_points]
plt.figure(figsize=(8, 8))
plt.scatter(x_vals, y_vals, s=1, color="blue")
plt.title("Hybrid D-ND Experiment: Linear and Fractal Phase")
plt.xlabel("Re(z)")
plt.ylabel("Im(z)")
plt.grid(True)
plt.show()
def run_simulation(params, iterations_slider, lambda_slider, threshold_slider, output_widget):
"""Runs the main simulation loop."""
R, all_points, linear_phase, ml_data, start_time, transition_time = initialize_system(params)
blend_phase = False
blend_counter = 0
with output_widget:
output_widget.clear_output(wait=True)
for t in range(1, iterations_slider.value + 1):
if linear_phase and not blend_phase:
R_next, all_points = run_linear_phase(R, all_points, params)
if check_stabilization(R, R_next, params):
transition_time = time.time() - start_time
ml_data.append([params.iterations, params.lambda_linear, params.transition_threshold, transition_time])
logging.info("Starting blending phase...")
linear_phase = False
blend_phase = True
R = R_next
else:
R = R_next
elif blend_phase and blend_counter < params.blend_iterations:
R, all_points = run_blended_phase(R, all_points, params, blend_counter / params.blend_iterations)
blend_counter += 1
else:
R_next, all_points = run_fractal_phase(R, all_points, params)
R = R_next
visualize_results(all_points)
# ==============================================================
# MAIN EXECUTION LOGIC
# ==============================================================
params = SystemParameters()
iterations_slider, lambda_slider, threshold_slider, output_widget = create_interactive_widgets(params)
# Attach callbacks
def on_slider_change(change):
run_simulation(params, iterations_slider, lambda_slider, threshold_slider, output_widget)
iterations_slider.observe(on_slider_change, names='value')
lambda_slider.observe(on_slider_change, names='value')
threshold_slider.observe(on_slider_change, names='value')
# Run initial plot
run_simulation(params, iterations_slider, lambda_slider, threshold_slider, output_widget)