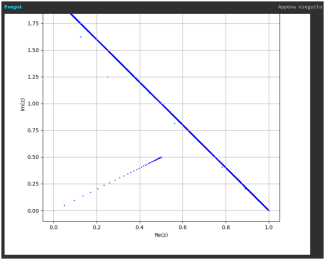
Osservando attentamente il grafico, possiamo identificare dettagli significativi relativi ai dati generati dal codice:

Cosa stiamo osservando nel grafico?

1. Punti generati nel piano complesso:
   • L'asse xx rappresenta la parte reale (Re(z)Re(z)).
   • L'asse yy rappresenta la parte immaginaria (Im(z)Im(z)).
   • I punti mostrano la traiettoria e le posizioni risultanti dalle iterazioni del sistema. Questi punti sono generati applicando trasformazioni lineari e frattali a un set iniziale.
2. Strutture presenti:
   • Linea diagonale: Questa può rappresentare una trasformazione lineare (ad esempio, f2_linearf2\_linear) che muove i punti verso un prototipo PP (un punto fisso nel piano complesso).
   • Cluster separati: Indicano le regioni in cui le trasformazioni frattali TAT_A e TBT_B hanno prodotto insiemi distinti, o una progressione nel passaggio tra fasi lineari e frattali.
3. Progressione iterativa:
   • Nelle prime iterazioni, i punti tendono a formare strutture più semplici e lineari, mentre con il passare delle iterazioni si sviluppano pattern più complessi, influenzati dalla casualità nelle trasformazioni (ad esempio, contrazioni con parametri casuali).

Analisi delle fasi del sistema

Il grafico rappresenta molto probabilmente il risultato delle due principali fasi:

1. Fase Lineare:
   • I punti iniziano a convergere verso PP, seguendo trasformazioni come f2_linearf2\_linear, dove ogni punto si avvicina a PP per una frazione λlinear\lambda_{\text{linear}}.
   • La diagonale potrebbe essere il risultato diretto di questa contrazione uniforme verso PP.
2. Fase Frattale:
   • Successivamente, i punti sono sottoposti a trasformazioni frattali (TAT_A e TBT_B), che contraggono e ruotano i punti verso offset AA e BB, rispettivamente.
   • La distribuzione più complessa in alcune aree potrebbe indicare l'azione iterativa delle trasformazioni frattali.

Conclusione

Questo grafico è una rappresentazione del comportamento del sistema D-ND che transita tra una fase lineare e una frattale:

• La diagonale potrebbe corrispondere alla fase lineare, dove i punti si allineano verso PP.
• Gli altri cluster o pattern più complessi indicano la fase frattale, dove i punti sono trasformati in base a contrazioni e offset.

Se vuoi, possiamo eseguire ulteriori analisi sul codice o modificare i parametri per ottenere altre visualizzazioni!

 

Image

 

 

import random
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import directed_hausdorff
from scipy.ndimage import measurements
import ipywidgets as widgets
from IPython.display import display
import logging
from multiprocessing import Pool
from sklearn.linear_model import LinearRegression
import time

# Initialize logging
logging.basicConfig(level=logging.INFO, format='%(asctime)s - %(levelname)s - %(message)s')

# ============================================================== 
# SYSTEM PARAMETERS CLASS
# ==============================================================
class SystemParameters:
   """Class to hold all system parameters."""
   def __init__(self, iterations=10000, transition_threshold=0.005, lambda_linear=0.1,
                P=complex(0.5, 0.5), alpha=0.4, beta=0.4, gamma=0.2, blend_iterations=5,
                scale_factor_A=0.5, scale_factor_B=0.5, offset_A=1j, offset_B=1):
       self.iterations = iterations
       self.transition_threshold = transition_threshold
       self.lambda_linear = lambda_linear
       self.P = P
       self.alpha = alpha
       self.beta = beta
       self.gamma = gamma
       self.blend_iterations = blend_iterations
       self.scale_factor_A = scale_factor_A
       self.scale_factor_B = scale_factor_B
       self.offset_A = offset_A
       self.offset_B = offset_B

# ============================================================== 
# TRANSFORMATION CLASS
# ==============================================================
class Transformation:
   """Class to represent a transformation."""
   def __init__(self, func, **kwargs):
       self.func = func
       self.kwargs = kwargs

   def apply(self, z):
       return self.func(z, **self.kwargs)

# ============================================================== 
# TRANSFORMATION FUNCTIONS
# ==============================================================
def T_A(z, scale_factor=0.5, offset=1j):
   """Transformation A: contraction towards (offset) with scale_factor."""
   return z * scale_factor + offset

def T_B(z, scale_factor=0.5, offset=1):
   """Transformation B: contraction towards (offset) with scale_factor."""
   return (z + offset) * scale_factor

def compose_transformations(z, transformations):
   """Composes a sequence of transformations."""
   result = z
   for transform in transformations:
       if isinstance(transform, Transformation):
           result = transform.apply(result)
       else:
           result = transform(result)
   return result

# ============================================================== 
# MAIN SYSTEM FUNCTIONS
# ==============================================================
def initialize_system(params):
   """Initializes the system with starting values."""
   R = {complex(0, 0)}
   all_points = set(R)
   linear_phase = True
   ml_data = []
   start_time = time.time()
   transition_time = None
   return R, all_points, linear_phase, ml_data, start_time, transition_time

def run_linear_phase(R, all_points, params):
   """Runs the linear phase transformations."""
   B = {complex(1, 0), complex(0, 2)}  # Example fixed set
   R_next = {z + params.lambda_linear * (params.P - z) for z in R}
   all_points.update(R_next)
   return R_next, all_points

def run_fractal_phase(R, all_points, params):
   """Runs the fractal phase transformations."""
   R_next = set()
   for z in R:
       if random.random() < 0.5:
           R_next.add(T_A(z, params.scale_factor_A, params.offset_A))
       else:
           R_next.add(T_B(z, params.scale_factor_B, params.offset_B))
   all_points.update(R_next)
   return R_next, all_points

def visualize_results(all_points):
   """Visualizes the results."""
   x_vals = [z.real for z in all_points]
   y_vals = [z.imag for z in all_points]
   plt.figure(figsize=(8, 8))
   plt.scatter(x_vals, y_vals, s=1, color="blue")
   plt.title("D-ND Model Visualization")
   plt.xlabel("Re(z)")
   plt.ylabel("Im(z)")
   plt.grid(True)
   plt.show()

# ============================================================== 
# EXECUTION LOGIC
# ==============================================================
params = SystemParameters()
R, all_points, linear_phase, ml_data, start_time, transition_time = initialize_system(params)

for t in range(1, params.iterations + 1):
   if linear_phase:
       R, all_points = run_linear_phase(R, all_points, params)
       if t > 100:  # Example condition to switch phase
           linear_phase = False
   else:
       R, all_points = run_fractal_phase(R, all_points, params)

visualize_results(all_points)
 

>>User: Pensi che queste osservazioni portano a qualcosa di utile?

Sì, queste osservazioni possono portare a risultati utili, soprattutto se inquadrate nel contesto di un modello come il Duale Non-Duale (D-ND), che ha lo scopo di esplorare transizioni tra stati o dinamiche complesse. Vediamo come:

1. Utilità nel contesto del Modello D-ND

• Comprensione delle Transizioni:
  • Le osservazioni sul grafico rivelano come il sistema evolve da uno stato ordinato (fase lineare) verso uno più complesso e dinamico (fase frattale). Questo è essenziale per modellare transizioni nel Continuum Nulla-Tutto (NT), uno dei pilastri del modello D-ND.
  • Può aiutare a formalizzare come gli stati passano da una condizione di stabilità a una di instabilità o complessità.
• Validazione delle Dinamiche:
  • Il comportamento osservato, come la formazione di cluster o la convergenza lungo determinate linee, può essere confrontato con le equazioni del modello. Questo aiuta a verificare se le trasformazioni (lineari e frattali) stanno funzionando come previsto.

2. Potenziali Applicazioni

• Ottimizzazione dei Sistemi Complessi:
  • I risultati possono essere applicati per ottimizzare sistemi che devono transitare tra stati diversi (es. modelli fisici, sistemi computazionali, dinamiche sociali).
• Simulazioni e Previsioni:
  • La capacità di generare e analizzare queste transizioni permette di simulare scenari complessi, prevedendo pattern di comportamento in contesti non lineari (ad esempio, in fisica teorica o in modelli di rete).
• Apprendimento Automatico:
  • I dati generati (distribuzioni e cluster) possono essere utilizzati come input per algoritmi di machine learning, migliorando la capacità di un modello di apprendere e predire dinamiche non lineari.

3. Direzioni Future

Per rendere queste osservazioni ancora più utili:

1. Quantificare i Pattern:
   • Misurare la dispersione, la densità e la distribuzione dei punti per ottenere parametri numerici che possano essere utilizzati per analisi quantitative.
2. Espandere le Trasformazioni:
   • Aggiungere nuovi tipi di trasformazioni o variare parametri come λ\lambda, offset e fattori di scala per esplorare ulteriori configurazioni del sistema.
3. Integrare Machine Learning:
   • Utilizzare il comportamento osservato per addestrare modelli predittivi, come già iniziato nel codice (es. regressione per stimare tempi di stabilizzazione).

Conclusione

Le osservazioni sul grafico non sono solo rappresentazioni estetiche, ma offrono una comprensione tangibile delle dinamiche del modello. Esse possono servire come base per:

• Validare il modello D-ND.
• Esplorare applicazioni pratiche in simulazioni complesse.
• Espandere il framework verso nuovi approcci analitici e predittivi.

Se queste osservazioni ti sembrano promettenti, possiamo ampliare ulteriormente il sistema o concentrare l'analisi su un particolare aspetto del comportamento.